안녕하세요, 오늘 다룰 내용은 전류 자계 무한직선 솔레노이드 이해 대한 내용입니다. 전류에 의한 자계이며, 그 중에 무한직선, 무한 솔레노이드, 환상 솔레노이드, 원형코일에 발생하는 자계에 대해서 나름대로 정리해서 설명 드리도록 하겠습니다.
1. 도체의 모양에 따른 자계의 방향과 크기
: 앞에 7장에서 제가 공부해서 설명 드린 내용은, 저희가 너무나도 잘 아는 자석에 의해 만들어진 자계를 공부한 것이라고 보시면 됩니다. (영구적으로 자석의 성질을 가지는 것을 “영구 자석” 이라고도 부릅니다.).
▼ 위에서 설명 드린 것처럼, 전류가 흐르는 도체의 모양별로 자계의 방향과 크기가 다양 해집니다.
첫 번째로 무한장 직선에 대해서 설명 드리면 무한장 직선의 뜻은 무한히 뻗은 직선형의 도체라고 생각하시면 됩니다. 이해를 돕기 위해서 아래 그림을 참조하시면 됩니다.
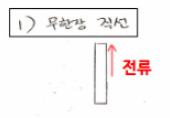
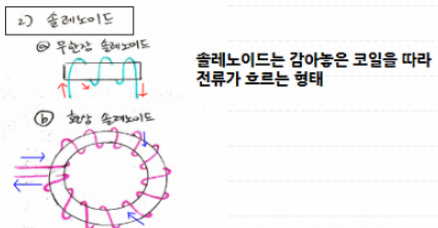
두 번째로 설명 드릴 내용은 솔레노이드입니다. 솔레노이드는 철심에 도체를 여러번 감아놓은 형태를 말하는 것입니다.
그리고 솔레노이드는 무한장 솔레노이드 그리고 환상(환형 솔레노이드)가 있습니다.
▼ 무한장 솔레노이드는 철심과 그것을 감은 코일이 일자로 무한히 긴 형태입니다.
그리고 환상(환형) 솔레노이드는 둥근 모양의 철심에 도체(코일)가 여러 번 감겨있는 형태입니다.
그리고 원형 코일은 원 모양으로 된 도체라고 생각하시면 됩니다. 이해를 돕기 위해서 아래 그림을 참조하시면 됩니다.
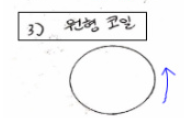
첨언으로 말씀드리면, 환상솔레노이드와 원형코일은 다른 물체입니다.
원형코일은 도체 자체가 원형이고 환상 솔레노이드는 원형의 철심에 도체를 감아놓은 형태입니다 마찬가지로 무한장 직선도체와 무한장 솔레노이드도 다릅니다.
자계를 만드는 방법은 영구자석 말고도 전류를 흘려주는 방법이 있습니다.
앙페르의 오른 나사 법칙에서 전류를 흘러주면, 그 주위에 자계가 생기는 법칙을 생각하시면 더 이해가 빠르게 되실 겁니다.
▼ 도체 모양에 따른 자계의 방향과 전류 방향에 따른 자계의 방향 (feat. 앙페르의 오른 나사 법칙)에 대해서 이어서 설명 드리도록 하겠습니다.
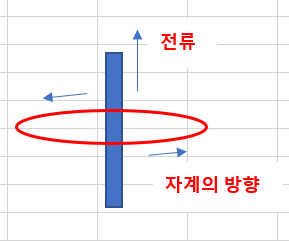
전류가 흐르는 방향과 자계(자기장)의 방향과의 관계를 나타내는 법칙입니다.
무한 직선도체에서 전류의 방향으로 오른손 엄지를 폈을 때 나머지 네 손가락이 감아지는 방향이 자계의 방향입니다.
또는 전류의 방향과 같은 방향으로 나사를 감아서 조일 때 그 감아지는 방향이 자계의 방향입니다.
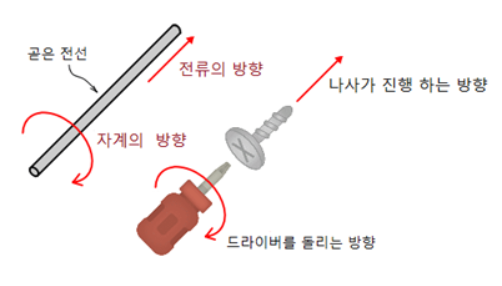
좀 자세히 설명 드리면, 도체에 전류를 흘려주면 주변에 자계가 생깁니다.
그리고 도체 모양별로 전류를 흘려 줄 때 생기는 자계의 방향과 크기가 다르게 나타납니다.
함께 보면 도움이 되는 글
▶ 전기자기학 3장 – 도체계의 합성 정전용량 + 콘덴서의 직렬 연결 + 병렬 연결
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전율 + 비유전율
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전체의 경계면 조건 + 경계면의 각도에 따른 전계와 전속밀도 + 전계와 전속밀도의 수직과 수평입사
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 전속선의 분포 + 유전체에 작용하는 힘 (맥스웰 응력)
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 콘덴서와 유전체를 같이 삽입한 콘덴서의 정전용량
▶ 전기자기학 5장 – 전기 영상법에 대해서 알아보자 + 무한평면 + 접지 구도체 + 점 전하
▶ 전기자기학 6장 – 전류에 대해서 알아보자 + 저항 (R) + 옴의 법칙 + 저항과 콘덴서 정전용량의 관계 + 누설전류 + 도체별 저항 + 저항과 정전
다음으로는 도체 모양에 따른 자계의 크기에 대해서 설명 드리도록 하겠습니다.
기본적으로 전류가 흐를때 자계가 생기므로 전류와 자계는 비례합니다. 또한 자계는 권수에도 비례합니다.
▼ 도체에 코일을 감은 횟수를 권수 또는 권선수라고 하고 공식에서 N으로 표현합니다.
보통 전기기사에서는 권선수를 조건으로 잘 주지 않기 때문에, “N = 1” 이라고 생각하고 문제를 푸시면 된다고 하네요.
1) 무한 직선
: 아래 수식에서 r은 직선 도체로부터의 거리입니다. 즉, 자계의 크기는 거리 r에 반비례함을 아실 수 있습니다.
그리고 앞에 설명 드린 대로, 전류에는 비례하죠.
– 무한 직선의 자계의 크기
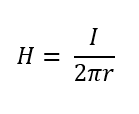
2) 무한장 솔레노이드
: 아래 “n” 은 단위 길이당 권수라고 이해하시면 됩니다. 코일 안쪽 철심 부분에서만 자계가 발생하고 외부의 자계 H=0입니다.
– 무환장 솔레노이드의 자계의 크기
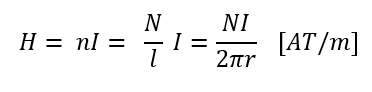
3) 환상 솔레노이드
: 이 때 r은 원 중심에서 철심부분의 중심까지의 거리입니다. 코일 안쪽 철심 부분에서만 자계가 발생하고 외부의 자계 H=0입니다.
환상 솔레노이드는 철심과 코일 부분보다 안쪽인 중심부도 코일 외부에 해당하므로 자계 H=0이 됩니다
▼ 무한장 솔레노이드와 환상 솔레노이드 모두 철심 내부에만 자계가 존재하며 내부의 자계(자장)는 평등자장, 균등자장입니다.
자계가 있는 공간 내에서는 균등하게 분배된다는 의미입니다
– 환상 솔레노이드의 자계의 크기
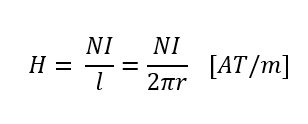
4) 원형 코일과 반원형 코일
: 위에서 1~3번 항목을 설명을 보시고 예상 했듯이, “a” 는 원형 코일의 반지름입니다.
즉 위에 1~3번항목도 마찬가지만, 지금까지 살펴본 자계 H의 공식을 자세히 보면 모두 전류를 거리로 나눠준 형태입니다. 반원형은 원형의 절반이기 때문에 2로 나눠 준거입니다.
▼ 전류의 단위로 [A] (암페어) 를 쓰는데 거리는 [m] 단위를 쓰므로 자계의 단위는 [A/m] 꼴이 됩니다.
또한 N이 공식에 대부분 포함되는데 권수로서 몇번 감았나(Turn)를 나타냅니다. 따라서 권수 개념을 포함한 일반적인 자계의 단위로 [AT/m]를 사용하는 것입니다.
– 원형 코일 자계의 크기
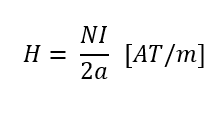
– 반원형 코일 자계의 크기
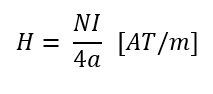
위에 설명 드린 내용을 요약을 다음과 같이 정리할 수 있습니다. 마무리 공부하시면 다시 한번 보시면, 머리에 들어오지 않을까 합니다.


함께 보면 도움이 되는 글
▶ 전기자기학 3장 – 도체계의 합성 정전용량 + 콘덴서의 직렬 연결 + 병렬 연결
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전율 + 비유전율
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전체의 경계면 조건 + 경계면의 각도에 따른 전계와 전속밀도 + 전계와 전속밀도의 수직과 수평입사
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 전속선의 분포 + 유전체에 작용하는 힘 (맥스웰 응력)
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 콘덴서와 유전체를 같이 삽입한 콘덴서의 정전용량
▶ 전기자기학 5장 – 전기 영상법에 대해서 알아보자 + 무한평면 + 접지 구도체 + 점 전하
▶ 전기자기학 6장 – 전류에 대해서 알아보자 + 저항 (R) + 옴의 법칙 + 저항과 콘덴서 정전용량의 관계 + 누설전류 + 도체별 저항 + 저항과 정전
이상입니다. 지금까지 전류 자계 무한직선 솔레노이드 이해 대해서 정리한 내용을 공유 드렸습니다.
요즘 과년도 시험에는 잘 안나오는 부분이라, 저도 그냥 지나갈까 했는데, 경험상, 과년도에서 안나오면 그 시험을 망한 거라는 걸 너무나도 잘 알기 때문에, 귀찮더라도, 하나 하나 빠지지 않고 공부하고 넘어가려고 합니다.
지루하시고, 확률이 낮더라도, 꼭 공부하고 가시라고 말씀드리고 싶네요! 그럼 오늘도 공부하느라고 수고 하셨고, 항상 말씀 드리지만, 같이 공부하고 같이 성장하지죠!
[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다. 검토 후 수정 및 삭제 조치 하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]









