안녕하세요, 이번 포스팅은 히스테리시스 곡선 및 자화곡선 B-H 곡선 관련 내용입니다. 즉 히스테리시스 곡선, 자화곡선, B-H 곡선에 대한 내용으로 작성해보도록 하겠습니다.
이 세 가지는 똑같은 의미를 가지고 있습니다. 그리고 히스테리시스곡선의 안쪽 면적이 히스테리시스손을 나타냅니다. 그럼 히스테리시스 곡선 및 히스테리시스 손에 대해서 포스팅을 시작해보도록 하겠습니다.
히스테리시스 곡선 및 자계와 자속밀도의 관계
: 히스테리시스 곡선은 자화곡선 또는 B-H곡선이라고도 합니다. 저도 처음에는 약간 헷갈렸습니다. 어떤 것은 히스테리시스 곡선이라고 비슷한 거 같은데 자화곡선이라고 했었거든요.
이 히스테리시스 곡선은 자계(H)와 자속밀도(B)의 관계를 나타내는 그래프입니다. 이 그래프를 이해하기 위해서 일단 아래 내용부터 설명 드리겠습니다.
– 자계와 자속밀도 관계
아래 B와 H의 관계식을 보면 자계가 세지면 그만큼 자속밀도가 커지는 것을 예상할 수 있습니다. 이 식대로라면, 자계가 계속해서 커지면 자속 밀도도 그만큼 게속해서 커질 것으로 생각할 수 있습니다. (기울기는 투자율 ‘μ’ 임)
B=μH
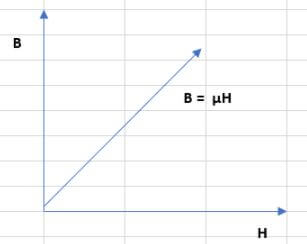
자계가 계속해서 커지면 자속밀도도 무한정 계속 커질 수 있을것 같은데 실제로는 그렇지 않다고 합니다.
자속밀도라는 것은 단위면적 1[m2]을 통과하는 자속 을 말하기 때문에 자계가 많아지면 자속도 그만큼 계속 많아지지만 1[m2]를 통과하는 자속의 양은 어느 순간 포화되서 더 증가하지 않고 일정한 값을 가질 것이라고 합니다.
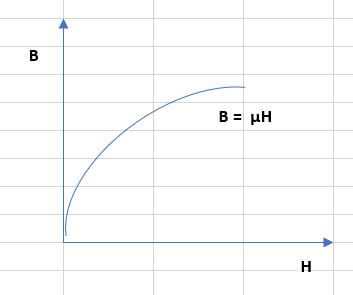
– 좀 쉽게 말씀 드리면 한정된 공간을 통과하는 화살이 늘어나다가 어느정도 시간이 지나면 그 화살이 지나가는 공간이 한정되어 있기 때문에 일정값 이상 증가하지 않는 것을 생각하시면 이해가 쉬우실 거 같습니다.
함께 보면 도움이 되는 글
▶ 전기자기학 3장 – 도체계의 합성 정전용량 + 콘덴서의 직렬 연결 + 병렬 연결
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전율 + 비유전율
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전체의 경계면 조건 + 경계면의 각도에 따른 전계와 전속밀도 + 전계와 전속밀도의 수직과 수평입사
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 전속선의 분포 + 유전체에 작용하는 힘 (맥스웰 응력)
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 콘덴서와 유전체를 같이 삽입한 콘덴서의 정전용량
▶ 전기자기학 5장 – 전기 영상법에 대해서 알아보자 + 무한평면 + 접지 구도체 + 점 전하
▶ 전기자기학 6장 – 전류에 대해서 알아보자 + 저항 (R) + 옴의 법칙 + 저항과 콘덴서 정전용량의 관계 + 누설전류 + 도체별 저항 + 저항과 정전
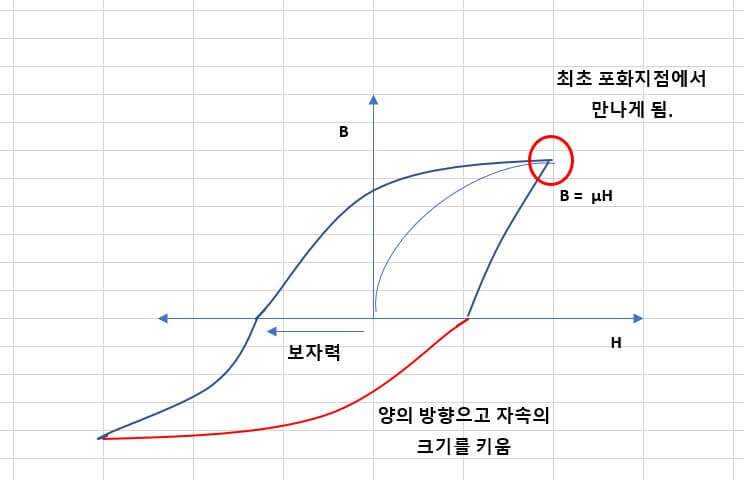
자속밀도 포화상태 및 잔류자기
– 자속 밀도 포화 상태
: 그러면 일정 크기의 자속 이후 자속밀도가 증가하지 않을 경우를 자속밀도 포화라고 생각하시면 됩니다.
이런 상태에서 자계를 서서히 줄여 ‘0’ 까지 줄이면 자속밀도도 ‘0’으로 줄어 들것으로 예상하실 수 있습니다. 하지만 ‘0’ 으로 줄어 들지 않습니다.
즉 자계가 ‘0’이 되더라도, 자속밀도는 어느정도 남아 있게 됩니다.
– 그 이유는 어떤 물체가 자계의 영향으로 인해 한 번 자석의 성질을 가지게 된 물체는 자계가 줄어 없어져도 자속밀도를 어느 정도 유지하기 때문입니다.
이 때 자계를 ‘0’ 으로 만들어도 남아있는 자속밀도를 ‘잔류자속밀도’ 또는 ‘잔류자기’ 라고 합니다.
– 잔류자기 제거
: 잔류자기를 제거하기 위해서는 자계를 ‘0’ 보다 작은 음수 방향으로 자계를 크게 하여 반대방향의 자속밀도를 만들면 원래 가지고 있떤 양수의 자속밀도와 상쇄되어 ‘0’이 되게 됩니다.
▼ 이 때 잔류자기를 없애기 위해 반대방향으로 가해주는 자계의 크기를 보자력이라고 합니다. 곡선과 횡축과 만나는 점의 크기가 보자력의 크기입니다.
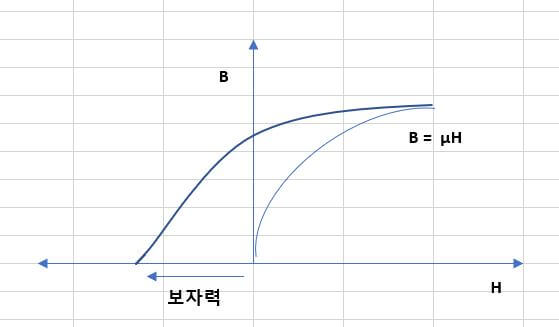
– 여기에서 계속적으로 반대방향으로 자속의 크기를 크게 해주면 잔류자기는 반대방향 즉 음의 방향으로 크기가 커집니다.
이것도 양의 방향에서 보여준 것 처럼 계속적으로 커지는게 아니고 어느정도 수준이 되면 포화에 이릅니다. 즉 증가하지 않는다는 애기죠.
– 이번에는 양의 방향으로 자계의 크기를 키워서 자속밀도를 ‘0’으로 만들려고 하지만 이 때도 양의 방향에서 보여준 것처럼 ‘0’이 아니고 어느정도의 잔류자기로 인해 ‘0’ 이 아닌 음의 방향의 자속밀도를 가지게 됩니다.
– 이때는 양의 방향으로 자계의 크기를 더 크게 키우면 잔류자기가 ‘0’이 되게 됩니다.
이때의 자속의 크기도 보자력이라고 합니다. (보자력은 잔류자기를 ‘0’으로 만들어주는데 필요한 자계의 크기라고 생각하시면 됩니다.)
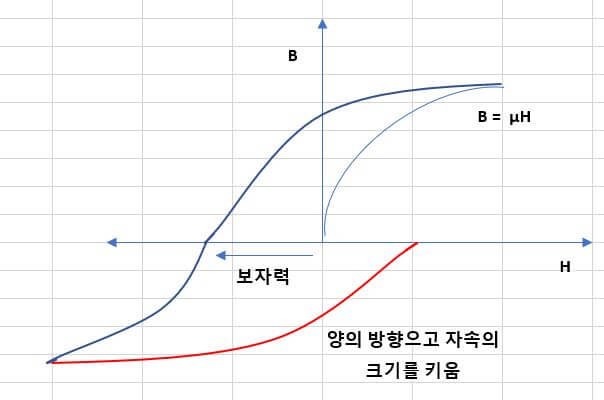
▼ 여기에서 양의 방향으로 자계의 크기를 계속 증가시면 자속밀도도 맨처음에 증가하던 방향으로 증가해서 최초 포화지점까지 증가합니다.
즉 최초 포화지점에서 만나게 되는 겁니다. 이렇게 형선 된 아래 빨간색로 이뤄진 곡선을 히스테리시스 곡선이라고 합니다.
히스테리시스손
: 잔류자기를 ‘0’으로 만들어 주기 위해 자계를 증가시키고 감소 시키는 과정 자체가 전류를 증가시키거나 감소시키는 것이라고 보시면 됩니다.
왜냐하면 자계는 전류의 흐름으로 인해 발생을 하기 때문입니다. 이 부분은 도체에 전류를 흘리면 앙페르의 오른나사 법칙에 따라 자계가 형성이 된다는 것을 생각하시면 쉽게 이해하실 수 있습니다.
– 이는 전류를 조절하는 과정에서 잔류자기가 생길 수 있다는 뜻입니다. 자계로 인해 자속밀도가 발생하고 잔류 자기로 인해 자계가 ‘0’이 되더라도, 자속밀도는 ‘0’이 되지 않으니까, 잔류 자가 발생 이유는 전류의 변화에 있다라고 생각하시면 될 거 같습니다.
– 잔류 자기로 인해 발생하는 손실을 히스테리시스손 이라고 합니다. 히스테리시스 곡선의 그래프에서 곡선으로 둘러싸인 부분이 면적이 히스테리시스 손실입니다. (위의 빨간색 선의 내부 면적이라고 생각하시면 됩니다.)
전류 흐름 – 자계 발생 – 잔류 자기 – 잔류 자기로 인해 손실이 발생 (히스테리시스 손)
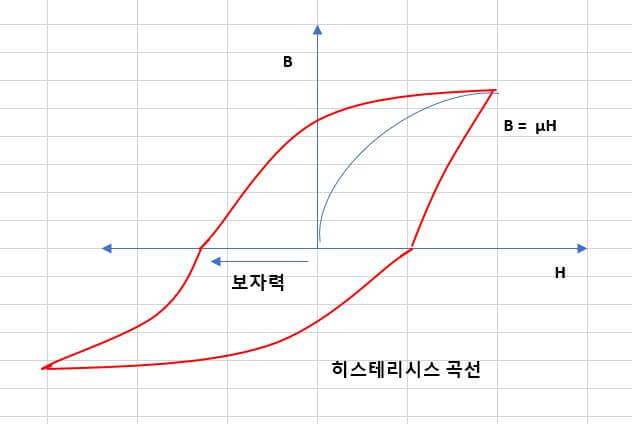
그래프의 개념으로 각자의 용어를 다시 설명 드리면 아래와 같습니다.
- 기울기 : 투자율(μ)
- 횡축(가로축) : 자계(H)
- 종축(세로축) : 자속밀도(B)
- 곡선과 횡축이 만나는 점 : 보자력
- 곡선과 종축이 만나는 점 : 잔류자기
- 곡선의 면적 = 히스테리시스 손실
함께 보면 도움이 되는 글
▶ 전기자기학 3장 – 도체계의 합성 정전용량 + 콘덴서의 직렬 연결 + 병렬 연결
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전율 + 비유전율
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 유전체의 경계면 조건 + 경계면의 각도에 따른 전계와 전속밀도 + 전계와 전속밀도의 수직과 수평입사
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 전속선의 분포 + 유전체에 작용하는 힘 (맥스웰 응력)
▶ 전기자기학 4장 – 유전체에 대해서 알아보자 + 콘덴서와 유전체를 같이 삽입한 콘덴서의 정전용량
▶ 전기자기학 5장 – 전기 영상법에 대해서 알아보자 + 무한평면 + 접지 구도체 + 점 전하
▶ 전기자기학 6장 – 전류에 대해서 알아보자 + 저항 (R) + 옴의 법칙 + 저항과 콘덴서 정전용량의 관계 + 누설전류 + 도체별 저항 + 저항과 정전
이상입니다. 지금까지 히스테리시스 곡선 및 자화곡선 대해서 포스팅을 작성하였습니다. 즉 히스테리시스 곡선과 곡선의 발생 원인 그리고 히스테리시스 손에 대해서 포스팅을 작성해보았습니다.
앞에서도 애기드렸지만, 히스테리시스 곡선은 자화곡선, B-H 곡선이라고도 합니다. 참조 하세요. 그럼 이만 마무리 하도록 하겠습니다. 감사합니다.
[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다. 검토 후 수정 및 삭제 조치 하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]









