안녕하세요, 이번 포스팅은 직렬 병렬 콘덴서 정전용량 대해서 정리한 내용입니다. 오늘 다룰 내용은 지난 번에 다룬 유전체에 대한 추가 내용입니다.
오늘 주로 설명 드릴 내용은, 콘덴서와 유전체를 같이 삽입한 콘덴서의 정전용량 에 대해서, 나름대로 정리해서 설명 드리도록 하겠습니다.
1. 공기로만 채워진 콘덴서와 유전체로만 채워진 콘덴서
: 이전 포스팅에 말씀 드린 대로, 유전체란 ‘전하가 움직이는 공간’ 중에 진공이나 공기를 제외한 다른 물질이라고 이해하시면 된다고 설명 드렸습니다.
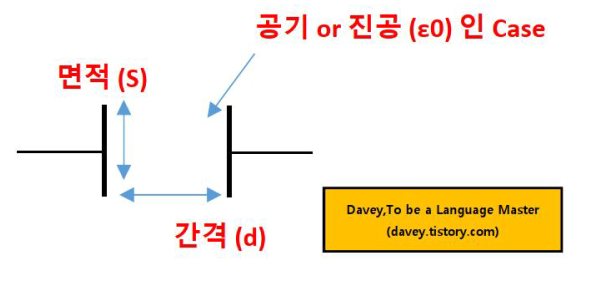
이전 설명 드린 공식으로 구현한 평행 평판 콘덴서의 정전 용량은 콘덴서 사이가 진공 또는 공기로만 되어있을 때의 공식입니다.
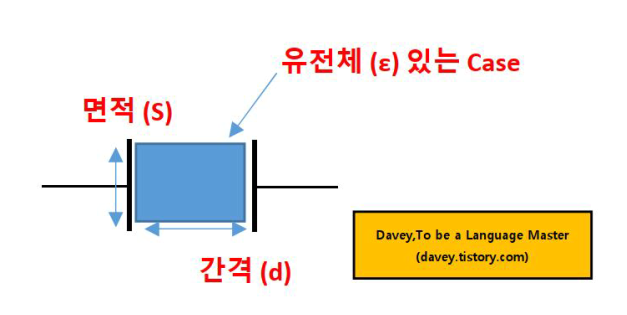
▼ 하지만, 유전율이 ε인 유전체가 콘덴서 사이를 채우고 있다면 정전용량은, ε0 대신 ε 이 되므로, 아래와 같은 공식을 구현해야 됩니다. (비유전율 : εs)
1) 공기로 채워진 콘텐서 경우의 평행 편판 콘덴서의 정전용량
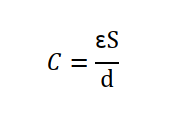
2) 유전체로 채워진 콘텐서 경우의 평행 편판 콘덴서의 정전용량
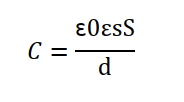
함께 보면 도움이 되는 글
▶ 전기자기학 1장 – 벡터의 이해 PART 2 + 벡터의 내적 + 벡터의 외적 + 벡터의 발산
▶ 전기자기학 2장 – 정전계 + 전자와 전류의 관계 이해
▶ 전기자기학 2장 – 유전율 + 투자율 + 빛의 속도 이해하기
▶ 전기자기학 2장 – 쿨롱의 법칙 + 전기 에너지 + 전기력 + 전계의 세기
▶ 전기자기학 2장 – 전하 + 전위
▶ 전기자기학 2장 – 전기력선 + 전속과 전속 밀도 그리고 전하밀도
2. 공기와 유전체가 혼합해서 채워진 콘덴서
: 위 1번의 경우에는 공기만 or 유전체로만 채워진 콘덴서의 콘덴서의 정전용량을 구했다면, 이번 경우에는 유전체와 공기 (or 진공)로 채워진 콘덴서의 용량을 구하는 법을 설명 드리도록 하겠습니다.
▼ 전제 조건은 공기 반, 유전체 반 이렇게 채워진 콘덴서의 정전용량을 구하는 걸로 하시죠.
이럴 경우에는, 공기로 채워진 부분의 정전용량과 유전체로 채워진 부분의 정전용량을 따로 계산한 뒤에 두 개의 정전용량을 합성해야 합니다.
그런데, 채워진 구조에 따라, 구하는 식도 달라집니다. 크게 채워진 구조는 직렬로 채워진 구조와, 병렬로 채워진 구조 이렇게 2가지로 구별할 수 있습니다.
1) 직렬 (간격을 나눌 경우)
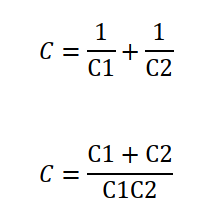
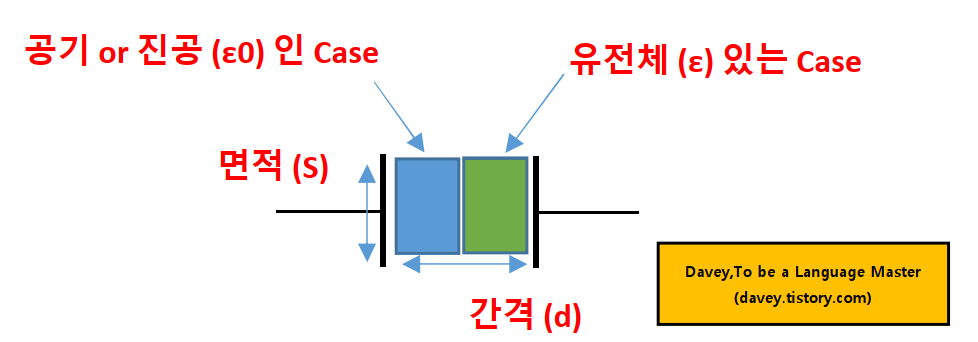
2) 병렬 (면적을 나눌 경우)
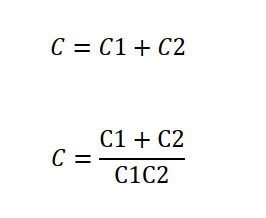
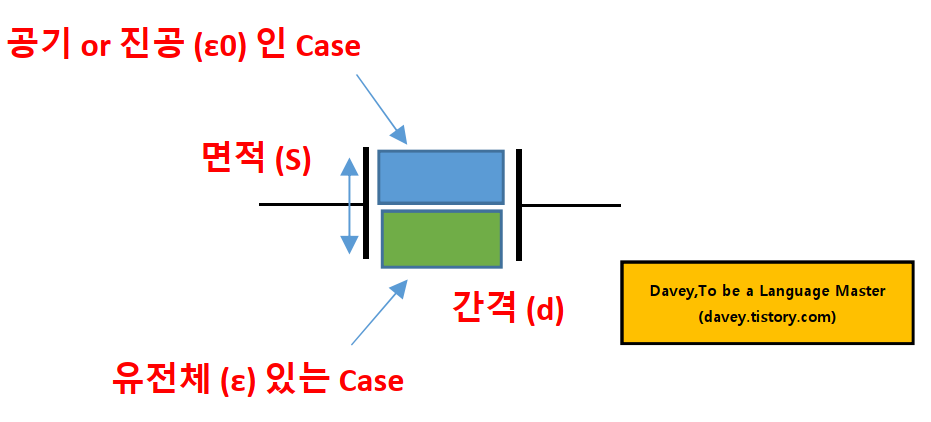
함께 보면 도움이 되는 글
▶ 전기자기학 1장 – 벡터의 이해 PART 2 + 벡터의 내적 + 벡터의 외적 + 벡터의 발산
▶ 전기자기학 2장 – 정전계 + 전자와 전류의 관계 이해
▶ 전기자기학 2장 – 유전율 + 투자율 + 빛의 속도 이해하기
▶ 전기자기학 2장 – 쿨롱의 법칙 + 전기 에너지 + 전기력 + 전계의 세기
▶ 전기자기학 2장 – 전하 + 전위
▶ 전기자기학 2장 – 전기력선 + 전속과 전속 밀도 그리고 전하밀도
이상입니다. 지금까지 직렬 병렬 콘덴서 정전용량 대한 내용으로 설명 드렸습니다. 콘덴서의 정전용량 부분이 정말 헷갈리기 쉬운 부분이라 이 부분만 중점적으로 정리를 하였습니다.
그림과 같이 공식을 이해하신다면, 더 이해하기 쉬우실 겁니다. 공부하면 할 수도록, 더 어려워지는 느낌과 이해를 하면 공식을 덜 외울 수 있겠구나 라는 안도감(?)이 동시에 들고 있습니다.
어렵다고 포기 하지 마시고, 저랑 같이 하나 하나 준비하며서, 공부해 나가시죠! 그럼 전기기사 다는 그날 까지 같이 공부하고 같이 성장하시죠! 감사합니다.
[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다. 검토 후 수정 및 삭제 조치 하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]









