정자계 자계 자기력선 자속밀도 – 전기자기학 7장

 안녕하세요, 오늘 다룰 내용은 정자계 자계 자기력선 자속밀도 대해서 나름대로 정리해서 설명 드리도록 하겠습니다. 쉬운 이해를 돕기 위해서 그림이나 공식도 추가하여 설명 드리도록 하겠습니다.

 

 

1. 정자계

: 정전계에서 “전” 를 “자” 짜로만 고치고 바라 보시면 더 공식 외우기도 쉽고, 이해하기도 쉬우 실겁니다. 하지만 전제는 정전계에 대해서 나름대로 이해가 되셨다는 전제입니다!

▼ 정자계는 ‘정지해 있는 자하들의 공간’ 이라고 이해하시면 됩니다. 자하란 자기적 성질을 가진 기본입자입니다.

(약간 전하를 설명할 때 같은 패턴으로 설명하신 거 눈치 채셨죠?!) 자하량은 m으로 나타내고 단위는 [Wb] (웨버) 라고 합니다.

 보통 자기는 자석의 형태로 다루는데요, 한쪽끝을 N극 다른쪽끝을 S극이라고 합니다.

자석 양극단의 세기인 자극의세기가 자하량에 의해 결정되므로 자하량과 자극의세기는 같은 것으로 봅니다. 전계의 세기도 전하량에 의해 결정되는 거와 비슷하다고 생각하시면 됩니다.

 

 

2. 쿨롱의 법칙 In 정자계

: 정자계에서의 쿨롱의 법칙을 설명을 드릴려고 합니다. 자석의 같은 극끼리는 반발력이 작용하고 서로 다른 극끼리는 흡인력이 작용합니다.

이 힘의 세기를 계산한 법칙이 쿨롱의 법칙입니다.

▼ 정전계, 정자계 두 쪽 모두 쿨롱의 법칙을 사용하게 됩니다.

 

 

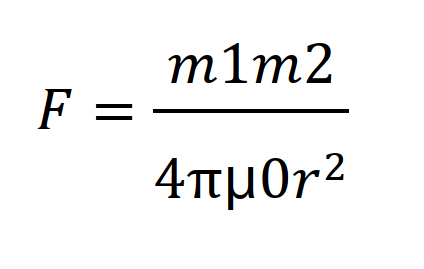
(m은 자하량 또는 자극의세기[Wb], r은 거리[m])

 

 

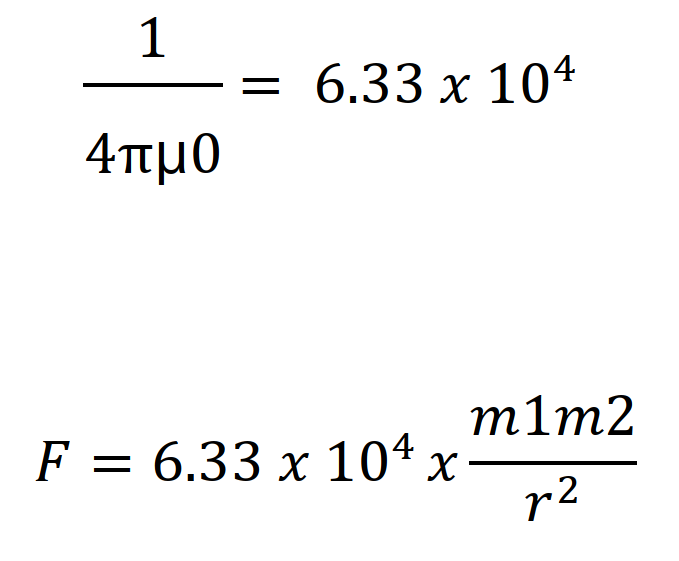
(거리 제곱에 반비례, 자하량의 곱에 비례)

 

 

 

 

 

 

3. 투자율

 : 2번 쿨롱의 법칙에서 보신 μ에 대해서 설명 드리도록 하겠습니다. 투자율을 기호로 μ 라고 사용합니다.

 전계에서의 유전율(ε)과 대응해서 이해하시면 더 도움이 되실 겁니다.

▼ 투자율이라는 의미는 ‘자하가 잘 투과되는 정도’ 라는 의미로 이해하시면 됩니다.

 

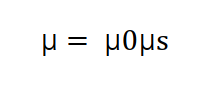
μ0는 진공,공기에서의 투자율로 나타냅니다.

 

 

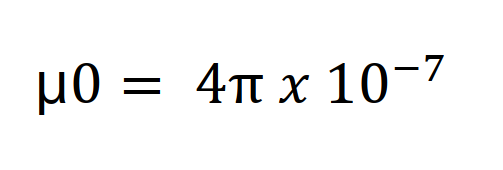
▼ μs는 비투자율로 매질마다 다르며 공기,진공에서의 몇 배인지를 나타냅니다 (진공,공기에서는μs = 1 입니다.)

 이어서 자계(H)에 대해서 설명 드리도록 하겠습니다. 쿨롱의 법칙 힘의 공식에서 두 자극의 세기(m) 중에 하나를 1[Wb]로 고정했을 때를 자계의 세기(H)라고 정의합니다.

 전계의 세기도, 두 전하 중에 하나를 “1[C]” 로 고정했을 때의 세기를 나타내는 것을 이해하시고 있다면, 이 정의 내용은 이해하기 쉬우실 겁니다.

▼ A는 암페어로서 전류와 관계된 단위임을 나타내고, – T는 몇번을 감았는지를 나타내는 용어입니다. 참조 하세요!

 

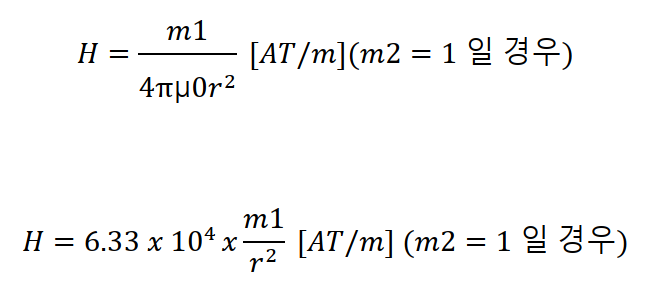
(단위 [AT/m]에서 AT는 암페어턴)

▼ 추가적으로 힘 F와 자계 H 사이의 식을 계산해보면 아래와 같은 공식을 유도 해 볼 수 잇습니다.

 

 

 

 

 

 

 

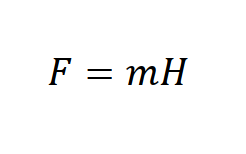
 다음으로는 자기력선에 대해서 설명 드리도록 하겠습니다.  전계의 전기력선과 대응하는 개념으로 자석의 자극에 의한 힘, 자계의 세기를 가상의 선으로 가시화시켜 나타낸 선입니다.

 전기력선과 조금 대비되는 것은 자석 주위에 철가루를 뿌렸을 때 철가루가 배열되는 형태를 통해 자기력선의 특징을 눈으로 볼 수 있다는 점입니다.

▼ 가장 큰 차이점은 발산과 회전입니다.- 전기력선은 발산만 할뿐 다시 돌아오는 회전은 하지 않습니다.

 하지만, 자석에 철가구를 뿌리면, 자기력선이 N극에서 나와서 S극으로 들어가는 형태를 보실 수 있습니다. 즉, 자기력선은 발산을 하지 않고, 회전을 합니다.

 

 

 

 

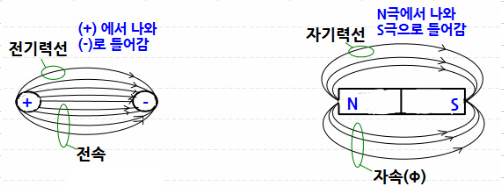
 마지막으로 자속과 자속밀도에 대해서 설명 드리도록 하겠습니다. 전기력선의 묶음을 전속이라고 했던 것 처럼, 자기력선의 묶음을 자속이라고 합니다.

 자기력선의 수가 매우 많아서 해석하기 복잡하므로 여러개를 한묶음으로 해석하는 것입니다. (전속을 설명할때와 똑같은 내용입니다.)

자속(Φ) = 자극의세기(m) (단위도 Wb로 동일합니다.)

 

 

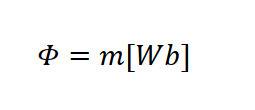
▼ 자속밀도(B)는 이런 자속을 면적으로 나눈 값으로, 다른 말로, 단위면적당 자속을 말합니다.- 일단 면적은 구의 면적을 가지고 설명 드리도록 하겠습니다. (S = 4πr2)

 

 

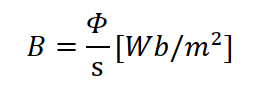
 자속과 자속밀도가 자계와 투자율과 어떤 관계를 가지게 되는지에 대한 공식을 나열해 보면Φ=BS 인 상태에서, Φ=m과 같고, 공간에서 자기력선은 구의 형태로 퍼져나가므로면적(S)에 구의 면적인 4πr2 을 대입하고 H의 식에서 μ0를 곱하면 다음과 같습니다.

 

 

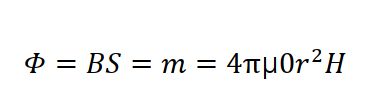
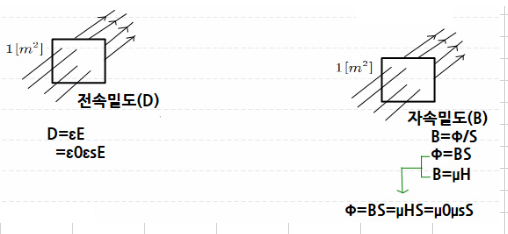
▼ 그러면 자속, 자속밀도 그리고 자계와 관계를 다시 종합하면 아래와 같습니다.

 

 

 

 

 

 

 이상입니다. 지금까지 정자계 자계 자기력선 자속밀도 대해서 정리한 내용을 공유 드렸습니다. 전계에 대해서 미리 공부를 해서 그런지, 약간 응용해서 공식을 생각하니까, 처음에 전계 공식을 이해했을 대보다는 더 수월하게 이해를 했던 거 같습니다.

 용어 자체가 헷갈리는 건지 아니면 이론 자체가 정리가 안된 건지는 모르겠지만, 간혹 혼돈이 되서, 이게 이건지를 혼자서 되씹는 과정이 아직까지는 필요한 상태인 거 같습니다.

 오늘도 공부하시느라 수고 하셨고, 계속 같이 공부해서, 같이 성장하시죠! 감사합니다.

 [참조 자료 출처 :  https://gongkachu12.tistory.com]

[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다. 검토 후 수정 및 삭제 조치 하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]