안녕하세요, 오늘 포스팅할 내용은 전기자기학 1장인 벡터의 이해 스칼라 단위 벡터 좌표계 정리 대한 내용입니다.
저를 포함한 많은 사람들이 자격증 추천 1위인 전기기사에 대해서 포스팅을 하려고 합니다.
포스팅하는 내용은 전기기사 기출문제를 풀기 전에 공부하시면 정말 많은 도움이 되실 겁니다.
[내용 업데이트 : 2024.01.17]
벡터와 스칼라
: 본론으로 들어가기 전에 말씀 드리면, “이론 – 과년도 풀기” 이 전기기사 필기 공부 방법 + 전기기사 실기 공부 방법의 정도 입니다.
저의 포스팅을 통해서, 자연스럽게 공부하는 방법도 익혀가시는 걸 추천 드립니다.
동시에 우리 일상 생활에서 뗄레야 뗄 수 없는 것 중에 하나인, “전기” 에 대해서도 포스팅 한다라고 생각하시면 됩니다.
누군가에는 필요한 학문이고, 누군가에게는 필요없는 학문일 수도 있습니다.
하지만 우리가 사용하는 전기에 대해서, 조금이나마 관심을 가지고 사용을 한다면, 더 유용하게 쓰지 않을까 하는 생각에서 시작해 보았습니다.
중간 중간에, 제가 설명한 부분에서, 빠진 것이나, 설명이 잘못 된 부분에 대해서는, 댓글 남겨 주시면, 감사 드리겠습니다.
그럼 오늘은 가장 기초인 벡터에 대해서 포스팅 해보도록 하겠습니다.
1) 스칼라(scalar)
: 하나의 실수값(real value)으로써, 어떤 물체의 무게, 속력, 온도, 부피, 저항, 전압, 전류 A, a를 나타 냅니다.
– 스칼라의 표기 방법
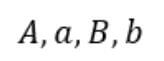
2) 벡터(vector) :
스칼라가 크기만 나타낸다면, 벡터는 어떤 성질의 크기와 방향을 모두 나타냅니다.
중력, 힘, 속도, 가속도, 전기장, 자기장 A 을 예로 들 수 있습니다.
– 벡터의 표기 방법 :
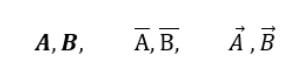
벡터 관련된 추가적인 설명일 필요하시면 네이버나 구글을 통해서 찾으실 수 있습니다.
함께 보면 도움이 되는 글
▶ 전기자기학 1장 – 벡터의 이해 PART 2 + 벡터의 내적 + 벡터의 외적 + 벡터의 발산
▶ 전기자기학 2장 – 정전계 + 전자와 전류의 관계 이해
▶ 전기자기학 2장 – 유전율 + 투자율 + 빛의 속도 이해하기
▶ 전기자기학 2장 – 쿨롱의 법칙 + 전기 에너지 + 전기력 + 전계의 세기
▶ 전기자기학 2장 – 전하 + 전위
▶ 전기자기학 2장 – 전기력선 + 전속과 전속 밀도 그리고 전하밀도
▶ 전기자기학 2장 – 가우스 적분형 + 미분형 + 푸아송의 방정식 + 라플라스 방정식
벡터를 나타내는 방법
직교 좌표계를 활용하여 벡터를 표현하는 방법은 크게 4가지로 나뉩니다.
그 종류는 아래와 같습니다.
1) 극형식으로 표현
: z = r ∠θ
2) 삼각함수 형식으로 표현
: z = r (cosθ + j sinθ)
3) 복소수 형식으로 표현
: z = x + jy
4) 오일러의 공식으로 표현
: z = r ejθ (e는 지수함수임)
직각 좌표계 대표식과 그래프는 아래 그림을 참조하세요. 그리고 추가적인 그래프는 구글에서 검색하시면 찾을 실 수 있습니다.
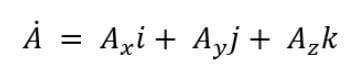
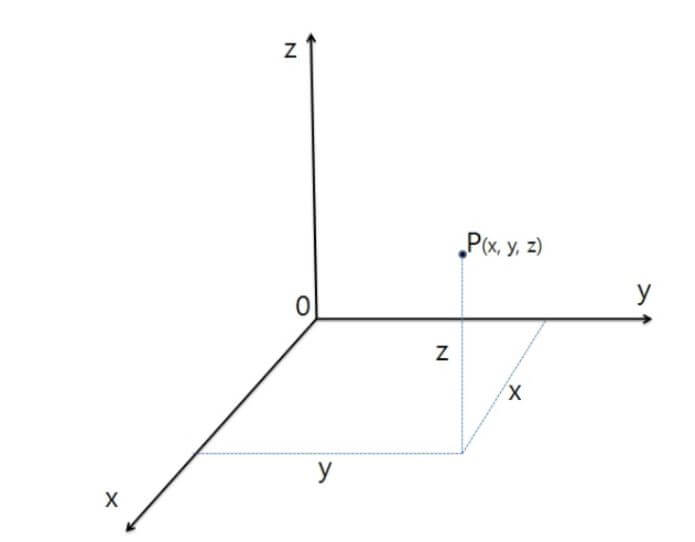
단위 벡터
: 벡터는 크기와 방향을 모두 나타 내는데, 방향만 나타내는 것을 단위 벡터라고 한다.
단위 벡터 구하는 공식은 아래와 같습니다.
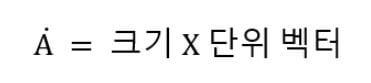
여기에서 단위 벡터를 구할려면, 벡터를 크기로 나눠주면 단위 벡터를 구할 수 있습니다.
즉, 벡터의 방향을 알려주는 단위 벡터를 알 수 있는 것입니다. 그리고 단위 벡터의 크기는 “1” 입니다.
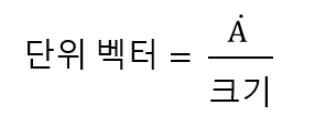
좌표계의 종류
1) 직각 좌표계
: 다른 말로, 직교 카트시안 좌표계 or데카르트 좌표계로 명명 합니다.
프랑스 수학자,철학자 René Descartes(데카르트, 라틴어 이름: Cartesius)가 최초로 도입로 도입 했으며, 직교 교차(서로 수직)하는 축에 대해 투영된 위치 좌표에 의해 위치가 결정되는 좌표계 입니다.
아래와 같이, 3개의 성분과 x, y, z 단위 기저벡터와의 선형결합으로 표현하는 좌표계입니다.
– 직각 좌표계 표현식

직각좌표계를 이용한 문제풀이 사항은 네이버에서 관련 서비스를 제공하는 여러 사이트를 찾으실 수 있습니다.
2) 원통 좌표계
: 2차원 극좌표계를 3차원으로 확장시킨 좌표계로서, 축방향 좌표 z 추가된 좌표계 입니다.
원통 좌표계를 표현하는 요소로는, ρ (수평거리), Φ (방위각,longitude), z (축방향 좌표) 가 있습니다.
– 직각 좌표계 구성하는 요소와 원통 좌표계를 구성하는 요소사이에 연관된 관계
: x = ρcosΦ, y = ρsinΦ, z = z
참고 사항
(1) 미소체적소 : dV = ρdρdΦdz
(2) 미소면적소 : dS = ρdρdΦ, dρdz, ρdΦdz (3가지 항목을 들 수 있음.)
원통좌표계를 이용한 문제풀이 사항은 네이버에서 관련 서비스를 제공하는 여러 사이트를 찾으실 수 있습니다.
3) 구 좌표계
: 2차원 극좌표계를 3차원으로 확장시켜 일반화시킨 좌표계로써, 구 좌표계를 표현하는 요소로는, r (원점 반경), θ (선택된 축에서 각도), Φ (그 축 둘레의 방위각) 이 있습니다.
– 직각 좌표계 구성하는 요소와 구 좌표계를 구성하는 요소사이에 연관된 관계
: x = r sinθcosΦ, y = r sinθsinΦ, z = r cosθ
r = √(x2 + y2 + z2), tanΦ = y / x, tanθ = √(x2 + y2) / z
– 참고 사항
1) 미소 입체각 : dΩ = sinθdθdΦ [sr]
2) 미소 면적소 : dA = r2 sinθdθdΦ [㎡]
3) 미소 체적소 : dV = r2sinθdrdθdΦ [㎥]
4) 구 전체 표면적 : A = 4πr2 [㎡]
함께 보면 도움이 되는 글
▶ 전기자기학 1장 – 벡터의 이해 PART 2 + 벡터의 내적 + 벡터의 외적 + 벡터의 발산
▶ 전기자기학 2장 – 정전계 + 전자와 전류의 관계 이해
▶ 전기자기학 2장 – 유전율 + 투자율 + 빛의 속도 이해하기
▶ 전기자기학 2장 – 쿨롱의 법칙 + 전기 에너지 + 전기력 + 전계의 세기
▶ 전기자기학 2장 – 전하 + 전위
▶ 전기자기학 2장 – 전기력선 + 전속과 전속 밀도 그리고 전하밀도
▶ 전기자기학 2장 – 가우스 적분형 + 미분형 + 푸아송의 방정식 + 라플라스 방정식
마무리
이상입니다. 지금까지 전기자기학 1장인 벡터의 이해 스칼라 단위 벡터 좌표계 정리 대해서 포스팅을 작성하였습니다.
정말 그냥 알고 있는 것을 설명하고, 손으로 쓰면 너무나도 간단한데, 타이핑을 해서 수식을 만드는 게 너무 시간이 많이 소요가 되네요.
그래프도, 손으로 그리면 되는데, 제가 그려보고, 너무 이상해서, 다른 그림을 참조 하였습니다.
구성 내용과 그림을 참 조하여, 공부하시면 더 도움이 되실 겁니다.
전기에 대한 포스팅의 첫 샆을 떴는데요, 솔직히 체감으로 너무 힘드네요. 위에 내용은 별로 없는 거 같은데, 거의 2시간 좀 안되게 포스팅 하는 데 시간이 걸린 거 같습니다.
하지만 이런 것도 하나 하나 배워나가는 과정으로 생각하도록 하겠습니다. 그럼 오늘도 공부하느라고 수고 하셨구요.
같이 공부해서 같이 성장하시죠! 감사합니다.
[저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다.
검토 후 수정 및 삭제 조치 하도록 하겠습니다. ]









