안녕하세요, 오늘 포스팅할 내용은, 벡터 관련 두 번째 포스팅으로 벡터의 내적 외적 발산 – 전기자기학 1장 대해서, 설명을 드리려고 합니다.
가장 기본적인 내용이지만, “이론 – 과년도 풀기” 이 전기기사 필기 공부 방법입니다. 즉 이론이 바탕이 되어야 합니다!
어떤 분들에게는 좀 헷갈릴 수 있는 거 같아서, 제가 가지고 있는 지식을 가지고, 최대한 자세히 설명을 드리도록 하겠습니다.
[내용 업데이트 : 2024.01.17]
벡터의 내적 (Vector Inner product)
: 벡터의 내적 외적 발산 내용 중에 벡터의 내적부터 설명 드리도록 하겠습니다.
벡터의 내적이란, 벡터가 표현되는 힘이 행한 일을 나타내는 값입니다. 즉, 임의의 벡터의 특정 방향을 가진 성분의 크기 벡터의 특정
방향, 성분, 투영(사영)의 크기, 일의 크기, 전류 밀도에 대한 전류의 크기 등을 구할 때 사용이 됩니다.
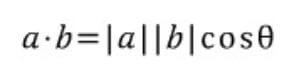
▼ 내적은, 전세계적으로 사용하는 용어로 애기하면, 스칼라곱(scalar product) 또는 dot product라고도 명명하며, 두 벡터의 크기와 두 벡터 사이의 각의 코사인 값을 곱한것으로 정의합니다.
결과는 스칼라양이 나오게 됩니다. 아래와 같이 수식으로 표현이 가능합니다.
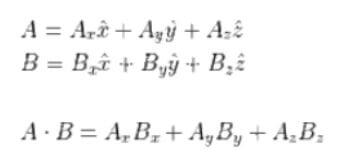
COS 의 각도가 0 일때는 “1” 이 되고, 90도 일때는 “0” 이 되는 걸 이해하기고, 아래 식을 보시면 더 이해가 빠르실 겁니다.
단위벡터를 이용한 내적 계산 설명입니다.
▼ 아래 식을 보면, 같은 축 (Ex, X, Y, Z축) 끼리 곱하게 되면, COS의 각도가 “0” 이므로, 그대로 스칼라 값이 나오지만, 다른 축과는 90도의 각도를 가지고 있으므로 “0” 됩니다.
벡터의 외적(outer product)
: 벡터의 외적이란, 벡터로 표현되는 넒이를 나타내는 값입니다.
즉 면 벡터의 표현, 토크, 각속도등을 구할 때 사용하며, 두 벡터에 수직인 벡터를 구한거나, 한 평면의 법선벡터(수직인벡터)를 구할 때, 유용하게 사용이 됩니다.
▼ 외적은 벡터곱(vector product) 또는 cross product 라고 명명하며, 두 벡터의 크기와 두 벡터 사이의 각의 사인값 그리고 수직인 벡터의 곱으로 나타냅니다.
아래와 같이 수식으로 표현이 가능합니다.
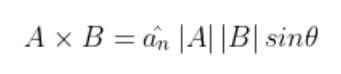
외적의 스칼라 값 (an) 은, A와 B에 서로 수직인 벡터인데, 그 방향은 A에서 B로 오른손으로 감쌀 때 엄지가 가리키는 방향이 됩니다.
전기를 기존에 공부하신 분들은 아시겠지만, 오른쪽 나사 법칙을 생각하시면 더 이해가 빠르실 겁니다.
▼ 내적과 다르게, 외적은, 2차원 공간이 아닌 3차원 공간으로 표현이 됩니다. 아래 그림 참조 부탁 드립니다.
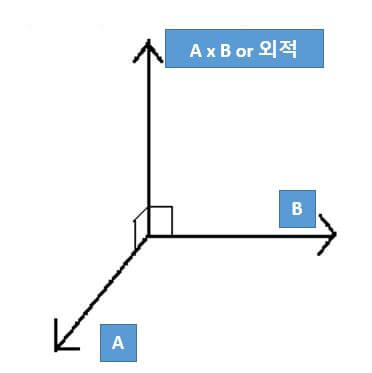
그리고 앞에 애기 드린 대로, 두 벡터가 표현하는 넒이입니다. 그럼 왜 위에서 설명드린 식이 나와있는지를 궁금해 하시는 분들이 계실 거라고 생각합니다.
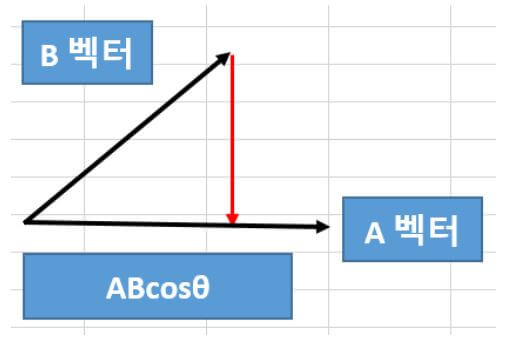
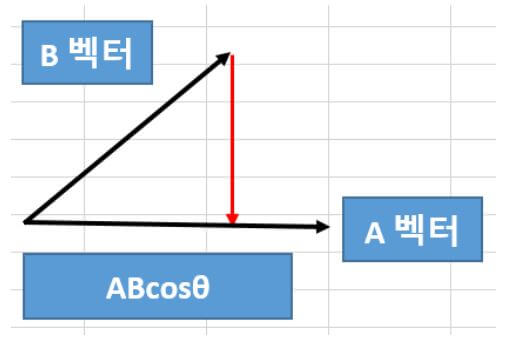
그래서, 아래 그림을 통해서, 어떻게 넒이를 구하는 식이, 위에 설명 드린 식대로 나왔는지를 설명 드리도록 하겠습니다. 일단 A, B벡터의 그림을 그려보면 아래와 같습니다.
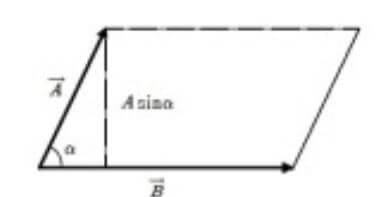
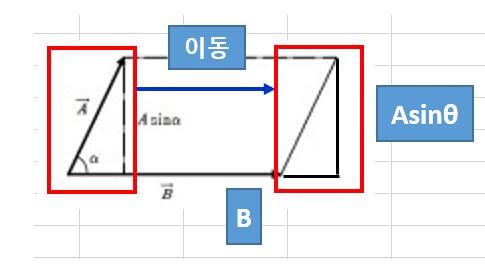
▼ 위 그림에서, 아래 Mark한 부분을 옮겨보면, A와 B벡터가 이루는 직사각형 (정사각형이 될 수 있음) 이 이뤄지면서, 넒을 쉽게 구 할 수 있는데, 세로의 길이가, Asinθ 라는 걸 참조 해주시면 됩니다.
스칼라의 기울기(Gradient)
벡터의 기울기란 임의의 위치에서의 기울기를 벡터로 표현하는 것입니다.
일단 벡터의 기울기를 설명하기 전에 미분에 대해서 간략하게 설명 드리도록 하겠습니다.
미분의 식으로 표현되는 결과 값은, 어떤 값에 대한 변화량을 나타내는 것입니다.
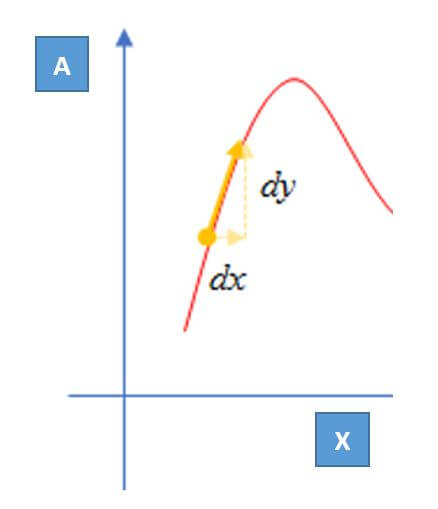
수식을 보면 d/dx나 d/dy로 쓸 수 있는데, 어떤 값의 기울기를 보는 거에 따라, 다르게 결과값이 도출이 됩니다.
예를 들어 설명 드리면, d/dx의 경우 x에 대한 변화량을, d/dy는 y에 대한 변화량을 구하는 것입니다.
아래 그림을 보시면, 더 이해가 잘 되실 거라고 생각합니다.
미분연산자는 삼각형을 거꾸로 쓴 형태인 ‘del’로 표시가 되며, 다른 이름으로는, ‘나불라’라고도 사용이 됩니다.
위에서 기본적인 수학적 미분기호 d와 다르게 라운드 ∂로 표현 되어 있는 이유는, 전자기학에서 x, y, z에 대해서 편미분을 하겠다 라는 의미로 라고 이해 하시면 됩니다.
편 미분이란, x와 y와 z가 서로간의 관계를 고려하지 않고 오로지 각각의 값에 대한 미분만 취하겠다는 의미로 이해 하시면 됩니다.다.
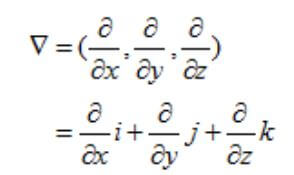
위의 미분연산자에 스칼라를 곱한 형태를 하면, 스칼라의 기울기를 구할 수 있습니다.
여기에서 잘 보셔야 되는게, 출력은 왜 벡터로 나오나면, 스칼라에 벡터인 미분연산자를 곱한 것이기 대문에, 결과는 벡터로 출력이 됩니다.
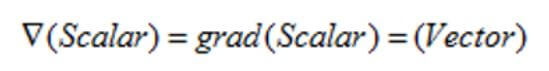
말 그대로, 스칼라의 기울기의 값을 벡터 형태의 출력을 해주는 것입니다.
fx, fy의 식을 아래와 같이 미분을 통해서, 기울기값을 알아 낼 수 가 있습니다.
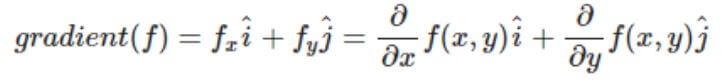
벡터의 발산
이어서 벡터의 내적에 대해서 설명 드리도록 하겠습니다. 어떤 벡터 함수에 미분연산자를 ‘내적’을 한 것으로, 기울기와 틀리게, 출력 값은 벡터가 스칼라 값을 출력 됩니다.
아래 식을 참조 하시면 됩니다. “div” 로 표현을 하며, “divergence” 라고 명명을 합니다.
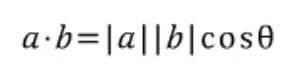
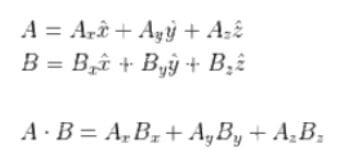
어떤 미소 공간 or 작은 공간에서, 벡터의 양이 증가하는지, 감소하는지를 볼 수 있으며, 증가하는 경우는 양수로 표현이 되며, 감소의 경우에는 음수로 표현이 됩니다.
“-” 말 그대로, 미분 연산자의 내적을 했으니, 각은 축의 COS 의 각도는 0이고, 0 일때는 “1” 이 되므로, 아래와 같이 스칼라 값을 출력이 되는 걸 확인 하실 수 있습니다.
아래 식은, 임의의 P, Q의 식을 발산했을 때의 식입니다.
벡터의 회전
이어서 벡터의 회전에 대해서 설명 드리도록 하겠습니다. 회전은 미분연산자를 다른 벡터 함수와 ‘외적’을 하는 것입니다.
쉬운 예를 들어서 설명을 해 드리면, 어떤 공간에 물체를 놓았을 때, 그 물체에 여러가지 힘이 가해져, 더 큰 힘에 의해, 그 물체가 돌아가게 됩니다.
▼ 이 힘의 크기와 방향을 나타내는 것을 벡터의 ‘회전(Curl)’이라고 이해하시며 됩니다. 간단한 식은 아래와 같습니다.
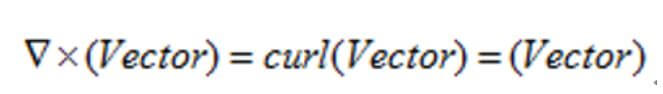
추가적으로, 표현식인 ∇×f 의 의미는 임의의 점 에서 벡터장이 향하는 정규화 시킨 수직 방향으로의 변화량이라고 설명하는 것을 이해하시면 됩니다.
더 쉬운 예를 들기 위해서 아래 식을 준비해보았습니다.
아래 식을 보시면, 임의 식에 회전(‘Curl’) 을 하게 되면, 각 축(벡터)에 맞게 배치가 됩니다.
첫번째 식을 보시면, 첫번째 열에는 벡터가 나오게 되고, 두번째 행은, 미분연산자 그리고 마지막은, 미분연산자와 회전을 하게 되는 또 다른 벡터 식이 나오게 됩니다.
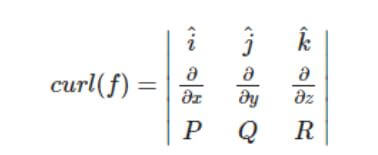
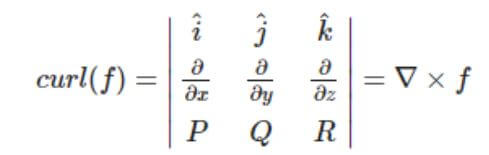
▼ 위 식을 아래와 같이 계산을 하면, 세번 째 식이 출력이 되는 걸 확인 하실 수 있습니다.

▼ 위 식 대로, 계산을 해보면, 아래와 같이 출력이 되며, 아래 식을 이용하여, 벡터의 회전 값을 출력 하실 수 있습니다.
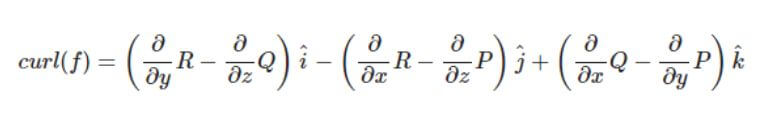
함께 보면 도움이 되는 글
▶ 전기자기학 1장 – 벡터의 이해 PART 1 + 스칼라 + 단위 벡터 + 좌표계.
▶ 전기자기학 2장 – 정전계 + 전자와 전류의 관계 이해
▶ 전기자기학 2장 – 유전율 + 투자율 + 빛의 속도 이해하기
▶ 전기자기학 2장 – 쿨롱의 법칙 + 전기 에너지 + 전기력 + 전계의 세기
▶ 전기자기학 2장 – 전하 + 전위
▶ 전기자기학 2장 – 전기력선 + 전속과 전속 밀도 그리고 전하밀도
▶ 전기자기학 2장 – 가우스 적분형 + 미분형 + 푸아송의 방정식 + 라플라스 방정식
마무리
이상입니다. 지금까지 벡터의 내적 외적 발산 – 전기자기학 1장 대해서 정리한 내용을 공유 드렸습니다.
기존에 알고 있는 지식을 설명을 하려고 하니까, 그게 더 어려운 거 같습니다.
그리고 공부하면서, 대충 넘어간 지식도, 글로 표현을 하려고 하니, 더 찾아 보게 되고, 제가 놓친게 없나 라는 생각도 하게 되는 과정이 였습니다.
수식을 그림으로 표현하는 것도, 시간이 많이 걸리긴 하네요.
하지만, 이렇게 저도, 하나 하나 머리에 정리해 나갈 수 있다라고 생각하고, 긍정적으로 작업을 하려고 합니다.
또한, 제 포스팅으로 인해, 어떤 분들에게는 도움을 드릴 수 있다는 걸로 보람차게 생각하도록 하겠습니다.
그럼 오늘도 공부하느라고 수고 하셨습니다.
같이 공부하고, 같이 성장하시죠. 감사합니다.
저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다.
검토 후 수정 및 삭제 조치 하도록 하겠습니다.
그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다.
게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.









